승호의 IT Hub
[회로이론] Part1_직류회로) Chap8_이차 회로 본문
8.1 서론
위 장에서는 2개의 에너지 저장소자를 포함하는 회로에 대해 살펴볼 것이다. 이러한 회로들은 그 응답을 기술하는 미분방정식이 이차 미분항을 포함하기 때문에 이차 회로로 알려져 있다.
이차 회로의 전형적인 예로는 세 종류의 수동소자로 구성된 RLC 회로가 있다. 다른 예로는 세 종류의 수동소자로 구성된 RL 회로와 RC 회로가 있다.


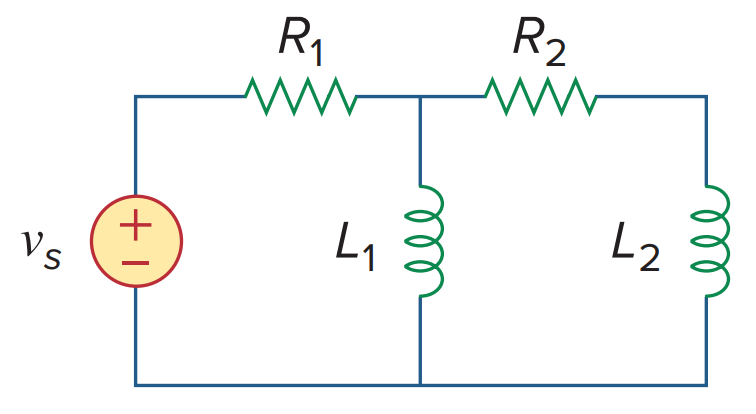
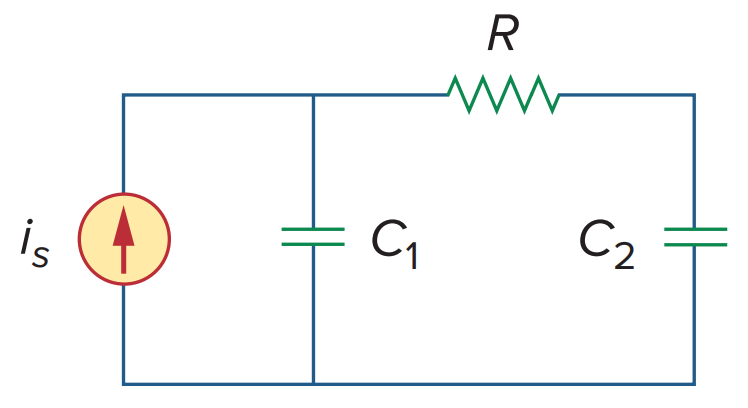
이차 회로는 이차 미분방정식에 의해 그 특성이 기술된다. 이것은 저항과 등가적인 에너지 저장소자 2개로 구성된다.
8.2 초깃값과 최종값 결정
이차 회로 해석에서 가장 큰 문제는 회로 변수의 초기 조건과 최종상태를 구하는 것이다. v와 i의 초깃값과 최종값은 쉽게 찾지만 도함수의 초깃값과 최종값(dv/dt & di/dt)을 찾는 데는 어려움을 느낀다. 그래서 이번 장은 v와 i의 초깃값, 최종값, 도함수의 초깃값, 최종값을 찾는 것을 중점으로 할 것이다.
| 초기 조건을 결정하는 데 유의해야할 점 |
| 1. 회로 해석에서 커패시터 양단에 걸리는 전압 v(t)의 극성과 인덕터에 흐르는 전류 i(t) 방향에 유의한다. |
| 2. 커패시터 전압은 항상 연속성이 있으므로 v(0+) = v(0-)이고 인덕터 전류도 항상 연속성이 있으므로 i(0+) = i(0-)이다. |
예제 8.1

8.3 무전원 직렬 RLC 회로

| 무전원 직렬 RLC 회로의 해석 |
| 직렬 RLC 회로는 커패시터와 인덕터의 초기 저장된 에너지에 의해 구동된다. 저장된 에너지를 인덕터의 초기 전류 I0와 커패시터의 초기 전압 V0로 표현한다.  |
루프에 KVL을 적용하면 |
적분항을 제거하기 위해 t에 대해 미분하고 항을 정리하면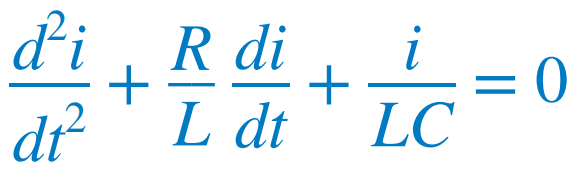 |
| 이것은 이차 미분방정식이며, RLC 회로를 이차 회로라 부르는 이유이다. |
커패시터의 초기 전압을 통하여 위 식을 또는 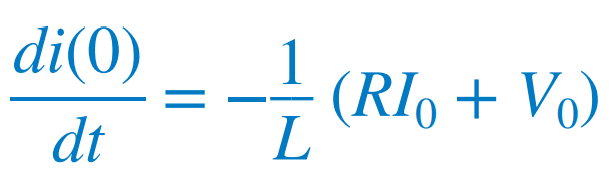 |
일차 회로에 대한 해석으로부터 결과는 지수 형태로 나타난다는 것을 알 수 있다.(사실 이차 미분방정식을 푸는 법을 안다면 더 쉽고 같은 결과를 낼 수 있다.)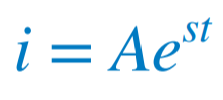 A와 s는 미지의 상수이다. 우리가 해석해야 할 식에 대입하고 미분하면 다음 결과를 얻을 수 있다. 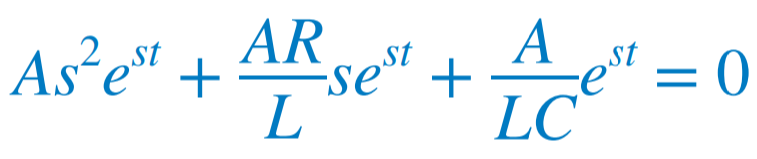 또는 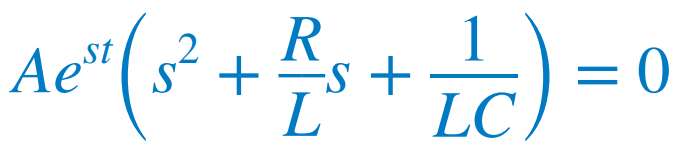 |
 이는 회로 해석을 위해 가정한 전류 해이므로 괄호 안의 식을 0으로 한다. |
근의 공식을 사용하여 s1과 s2를 구할 수 있다. 또한 이 이차 방정식은 근이 i의 특성을 나타내므로 특성방정식이라 일컫는다.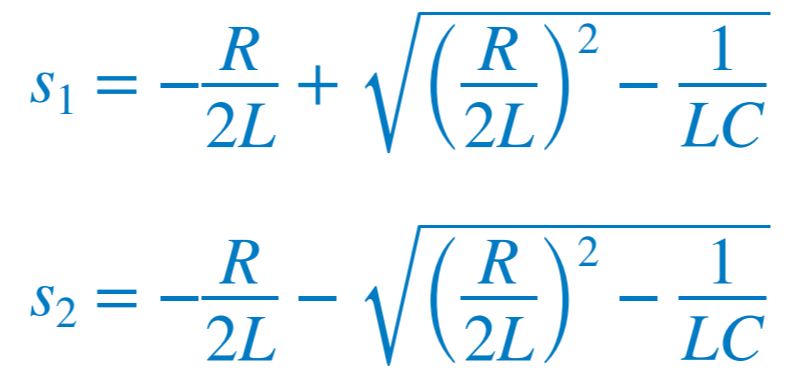 근의 표현을 더 간략화하면 다음과 같이 나타낼 수 있다. 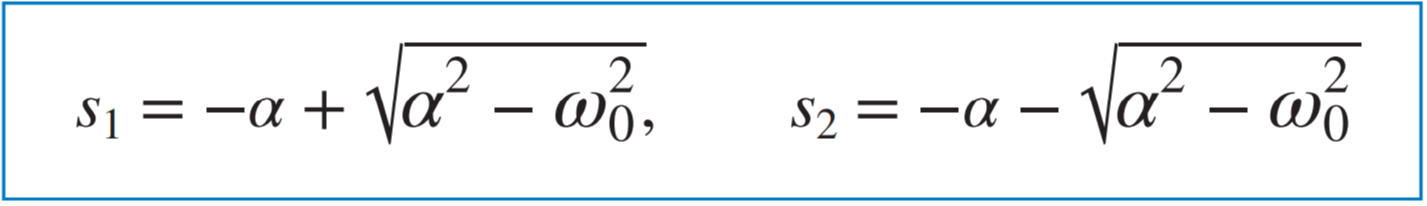 ★여기서 α는 감쇠 계수(or 네퍼주파수), ω0는 공진 주파수(Resonant frequency)(or 부족제동상태의 고유주파수)라 한다.★ 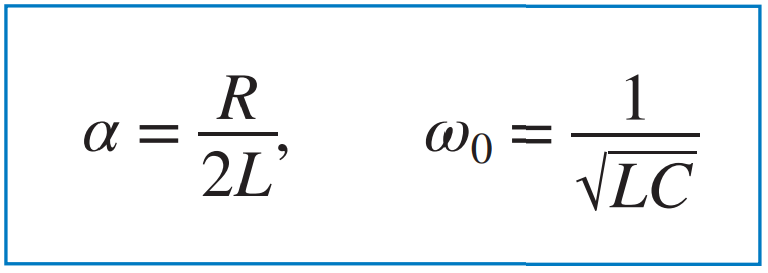 |
| s의 값이 2개임을 보아 i에 대해 가능한 해가 두 가지 있음을 의미한다. i를 가정하면 i는 선형 합성을 통해 구할 수 있다. 직렬 RLC 회로의 자연응답은 이후의 A와 s의 값들은 초깃값을 통해 결정된다. |
★이제부터 설명할 내용은 내가 생각하기에 이차 회로에서 중요한 부분 중 하나라고 생각한다.★
직렬 RLC 회로의 자연응답에서 α와 ω0의 값에 따라 3가지 형태의 해가 있다.
1. α > ω0일 때 응답은 과제동이다.
2. α = ω0일 때 응답은 임계제동이다.
3. α < ω0일 때 응답은 부족제동이다.
| 과제동(α > ω0) |
과제동은 전형적인 RLC 회로의 자연응답이다.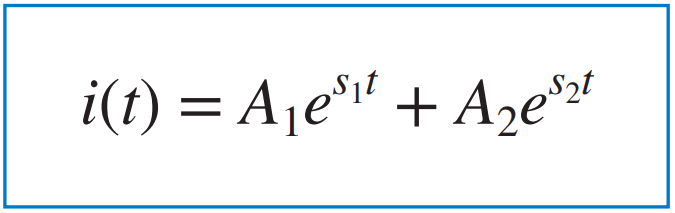 |
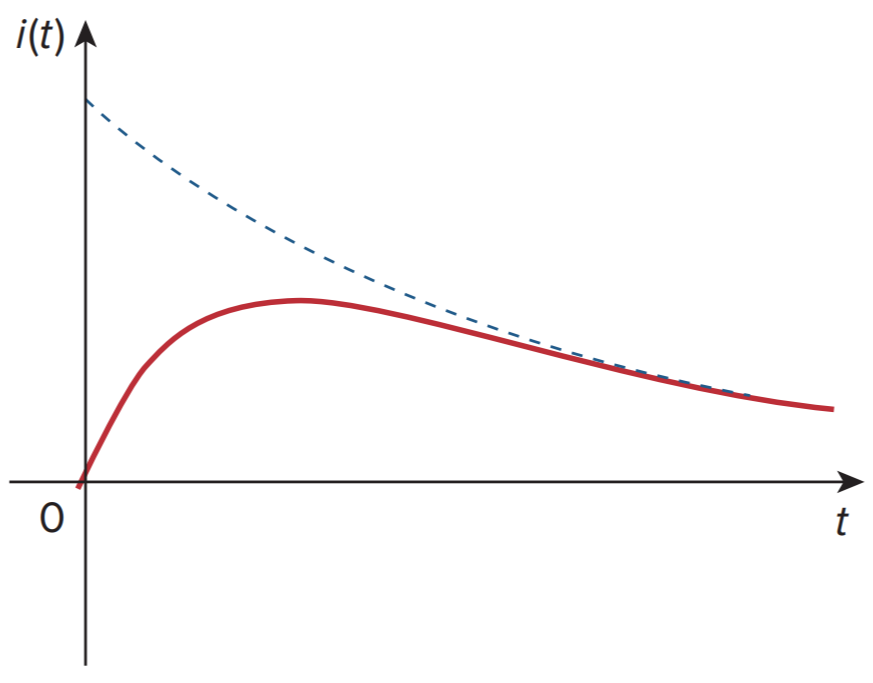 |
| 임계제동(α = ω0) |
| 임계제동일 때에는 s1 = s2 = -α = -R/2L 이러한 경우  그치만 두 초기 조건은 하나의 상수 A3로 충족될 수 없다. |
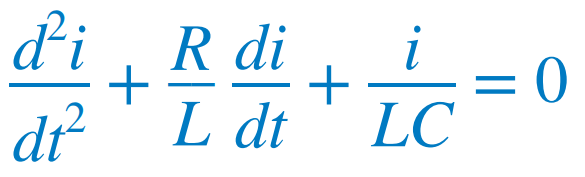 위 식으로 돌아와서 α = ω0 = R/2L을 이용하여 다음과 같은 식을 도출할 수 있다.  또는  |
다음과 같이 치환하면, 위와 같이 된다.  |
치환한 식을 다시 보자면 f = A1e^-αt를 가진 일차 방정식으므로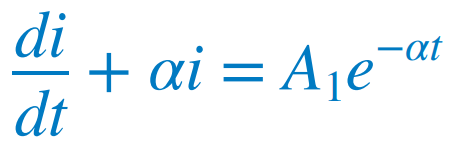 또는  이는 다음과 같이 다시 적을 수 있다. 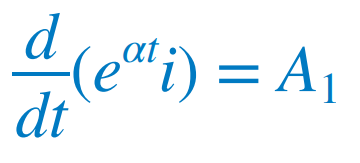 양변을 적분하면  또는  A2는 또 다른 상수이다. 임계제동 회로의 고유응답은 두 항의 합이 된다. 음의 지수함수와 선형항을 곱한 음의 지수함수이다.  |

| 부족제동(α < ω0) |
α < ω0일 때 C < 4L/R^2이다.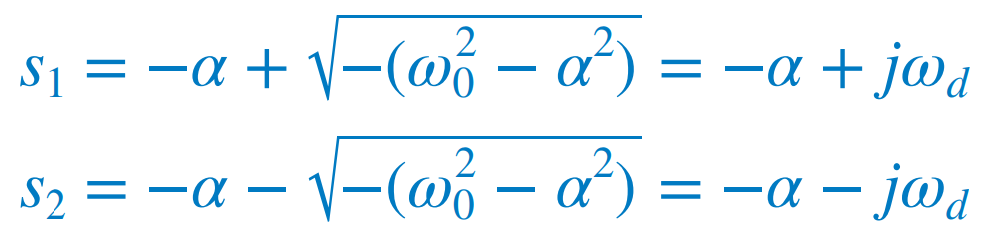 여기서 ωd^2 = ω0^2 - α^2이고 감쇠주파수라고 불린다. ω0는 자연응답을 결정하는 데 도움을 주기 때문에 무감쇠 고유주파수라 부르고 ωd는 감쇠 고유주파수라 부른다. |
고유응답은 아래 식처럼 되고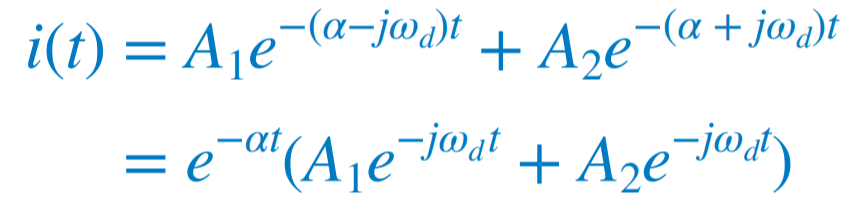 위를 오일러의 정리를 이용하면  다음과 같은 식을 얻을 수 있다.  |
A1과 A2는 상수이므로 B1 = A1 + A2, B2 = j(A1 - A2)로 치환하면 다음과 같은 식을 얻을 수 있다.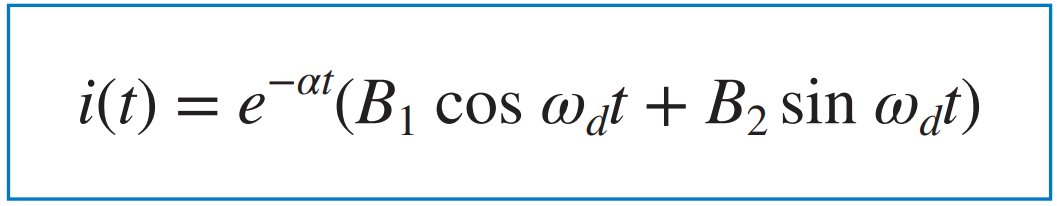 |
예제 8.4

8.4 무전원 병렬 RLC 회로

| 무전원 병렬 RLC 회로의 해석 |
초기 인덕터 전류를 I0, 초기 커패시터 전류를 V0라고 가정하자. |
3개의 소자가 병렬로 연결되어 있으므로 모두 동일한 전압 v가 양단에 걸린다. 회로 상단에 KCL을 적용하면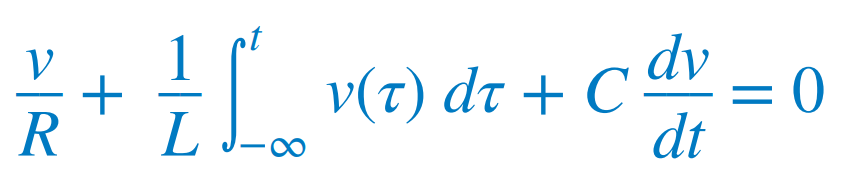 t에 대해 미분하고 C로 나누면  |
이차 미분은 s^2로, 일차 미분은 s로 치환함으로써 특성방정식을 얻을 수 있다.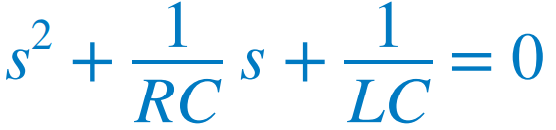 특성방정식의 근은 아래식 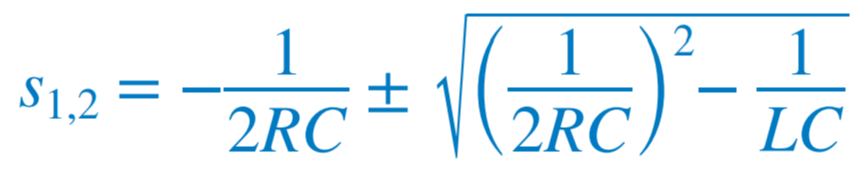 또는  과 같이 나타낼 수 있다. |
여기서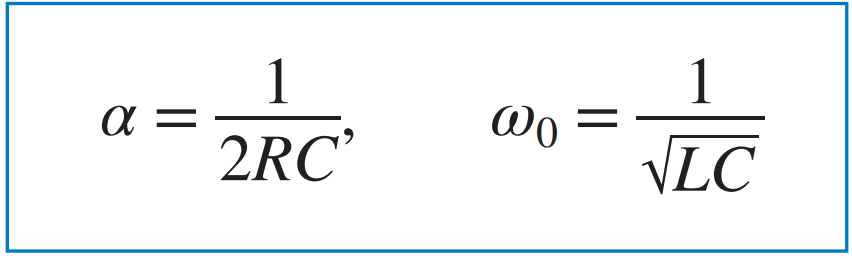 위와 같이 정리할 수 있다. |
| 과제동(α > ω0) |
α > ω0일 때, L>4R^2C이다. 특성방정식의 근은 음의 실수이며 응답은 아래 식과 같다. |
| 임계제동(α = ω0) |
α = ω0일 때 L = 4R^2C이다. 근은 실수이고 동일한 값을 가지므로 응답은 아래와 같다. |
| 부족제동(α < ω0) |
α < ω0일 때, L < 4R^2C이다. 이 경우 근은 복소수이고 다음과 같이 표현된다.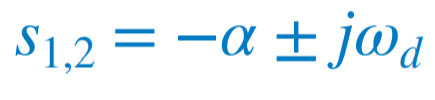 |
여기서 ωd는 아래와 같이 표현된다.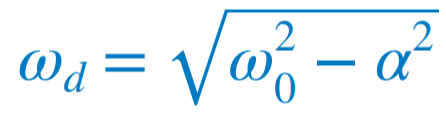 |
응답은 아래 식과 같다. |
예제 8.6

8.5 직렬 RLC 회로의 계단응답

| 직렬 RLC 회로의 계단응답 해석 |
계단응답은 직류 전원의 갑작스러운 공급에 대한 반응이다. 회로에 t > 0일 때 KVL을 적용하면 아래 식을 얻을 수 있다.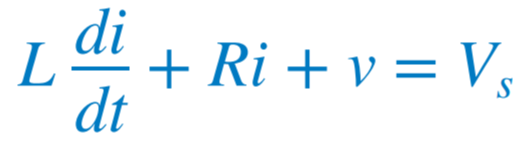 그리고 전류는 다음과 같이 표현할 수 있다. 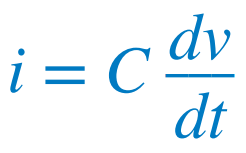 |
전류를 대입하고 식을 정리하면 아래와 같다.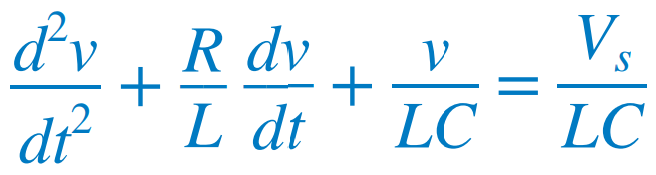 |
| 전에 무전원 RLC 회로의 해석을 보면 우측 항이 0인 것만 제외하고는 형태가 같은 것을 알 수 있다. 이를 좀 더 명확하게 말하자면 계수는 같고(주파수 파라미터를 결정하는 데 중요하다) 변수는 다르다. 이를 통해 알 수 있는 사실은 직렬 RLC 회로의 특성방정식은 직류 전원의 존재에 따른 영향을 받지 않는다는 것을 알 수 있다. 위 식에는 두 가지 요소, 과도응답 Vt(t)와 정상상태 응답 Vss(t)가 있다. 즉  과도응답의 형태는 무전원 회로의 해와 같다. 그러므로 과도응답 Vt(t)의 과제동, 부족제동, 임계제동은 각각 아래와 같이 나타낼 수 있다. 과제동 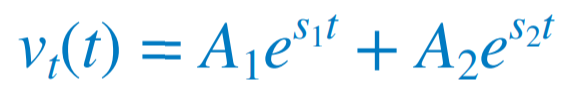 임계제동  부족제동 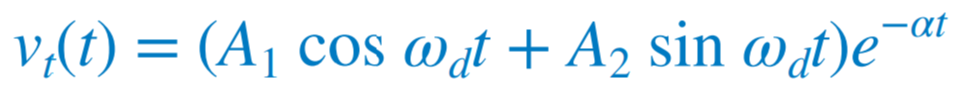 |
정상상태 응답은 v(t)의 최종값이다. 회로에서 커패시터 전압의 최종값은 전원 전압 Vs와 같다. 그러므로 |
과제동, 임계제동, 부족제동의 경우에 대한 완전해는 아래와 같이 정리할 수 있다.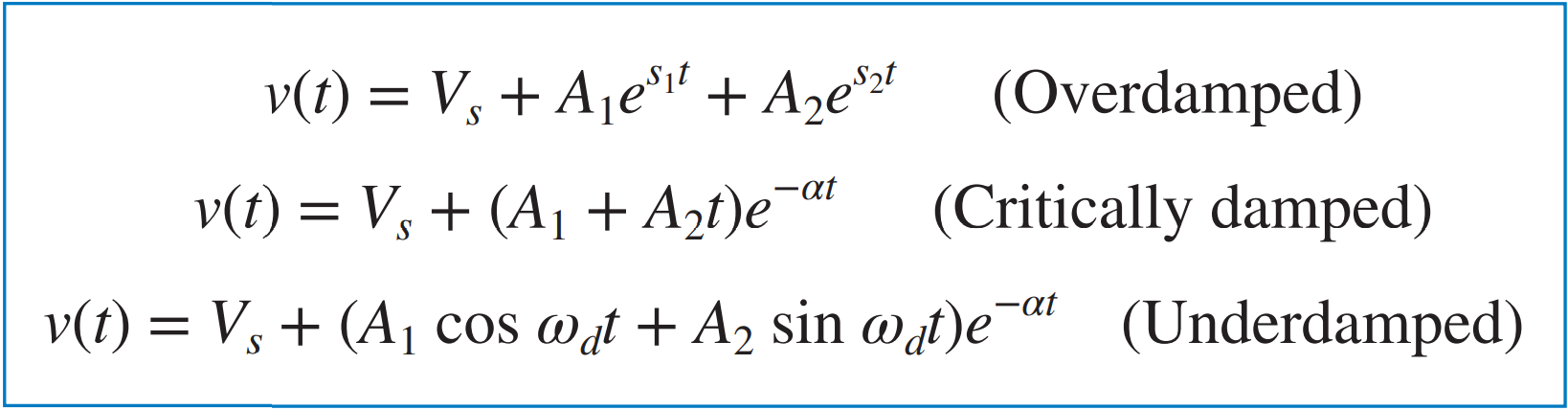 |
예제 8.7

8.6 병렬 RLC 회로의 계단응답
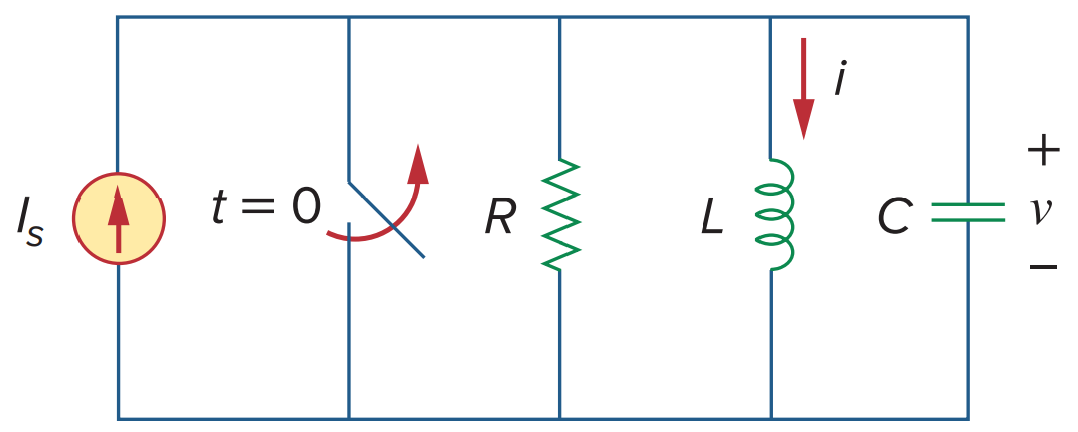
| 병렬 RLC 회로의 계단응답 해석 |
t > 0일 때 회로의 위쪽 노드에 KCL을 적용하면 아래 식을 얻을 수 있다. 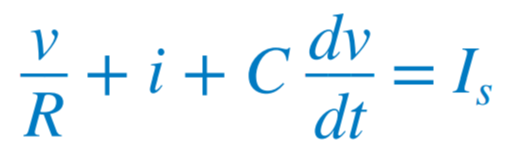 그리고 전압은 다음과 같이 표현할 수 있다. 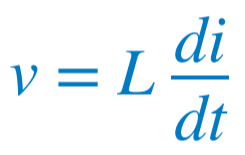 |
전압을 대입하고 식을 정리하면 아래와 같다.  |
| 위 식을 보면 직렬 RLC 회로의 계단응답 해석과 같은 형태의 식이란 것을 알 수 있다. 완전한 해는 과도응답 it(t)와 정상상태 응답 iss(t)로 이루어진다. 즉  |
과제동, 임계제동, 부족제동의 경우에 대한 완전해는 아래와 같이 정리할 수 있다. 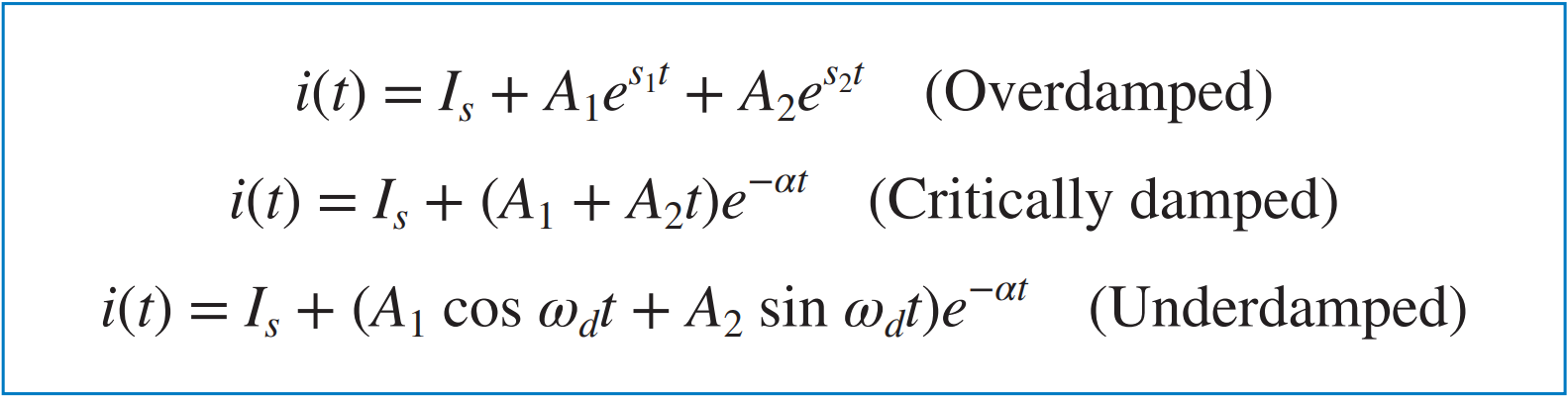 |
예제 8.8

'회로이론' 카테고리의 다른 글
| [회로이론] Part2_교류회로) Chap10_정현파의 정상상태 해석 (0) | 2024.04.03 |
|---|---|
| [회로이론] Part2_교류회로) Chap9_정현파와 페이저 (0) | 2024.04.01 |
| [회로이론] Part1_직류회로) Chap7_일차 회로 (0) | 2024.02.24 |
| [회로이론] Part1_직류회로) Chap6_커패시터와 인덕터 (0) | 2024.02.24 |
| [회로이론] Part1_직류회로) Chap4_회로 해석을 위한 정리 (0) | 2024.02.22 |




