[회로이론] Part2_교류회로) Chap9_정현파와 페이저

9.1 서론

위 장에서는 교류회로를 대상으로 회로 해석을 살펴볼 것이다. 교류 시스템은 장거리에 걸쳐 보다 효율적이고 경제적으로 전송할 수 있는 이점이 있다. 이 장에서는 특히 교류 시변 동작, 즉 정현파에 구동되는 회로를 살펴볼 것이다.

정현파는 사인함수와 코사인함수의 형태를 가진 신호이다.

9.2 정현파

v(t) = V_msin(ωt)

V_m = 정현파의 진폭

ω = 각주파수(rad/s)

ωt = 정현파의 편각(argument)

정현파를 편각의 함수로 표현	정현파를 시간의 함수로 표현

 

정현파

위 그림을 통해 주기를 알 수 있다.

v(t)가 T초마다 반복된다는 사실을 통해 t를 t+T로 치환할 수 있다.

고등학교 물리 시간에 파장에 대해서 배운다면 파장은 주기적이라는 사실을 알 수 있다. 그러므로 v(t)를 주기적이라고 일컬을 수 있으며 정현파에 대해서 밑에와 같이 정의할 수 있다. 주기함수는 모든 t와 모든 정수 n에 대해 f(t) = f(t + nT)를 만족한다.

주기의 역수는 시간당 사이클 수가 되며, 이를 정현파의 주기주파수 f라 일컫는다.

이제 정현파를 보다 일반적인 형태로 표현해보자. 여기서 (ωt + Φ)는 편각이고, Φ는 위상이다.

두 정현파를 그림으로 나타내면 아래와 같다. 이 경우에는 "v2가 v1보다 Φ만큼 앞선다" 또는 "v1이 v2보다 Φ만큼 뒤진다"고 한다.

정현파는 사인 또는 코사인 형태로 표현될 수 있다. 2개의 정현파를 비교할 때, 양의 진폭값을 가진 코사인 또는 사인으로 표현하는 것이 편리하다. 이러한 비교를 위해 다음의 삼각함수 공식을 이용할 수 있다. 이상의 관계식으로부터 다음이 쉽게 증명될 수 있다. 이러한 관계를 이용하여 임의의 정현파를 사인 형태에서 코사인 형태로 상호 변환할 수 있다.

코사인 형태 정현파 합성의 크기와 편각은 밑의 삼각함수 공식으로 통해 쉽게 구할 수 있다. 3cos(ωt)와 4sin(ωt)로 예시를 들 것이다. 여기서 C와 θ는 아래와 같이 정리할 수 있다. 이를 이용하면 어느 정현파든 변경하고 합성할 수 있다.

9.3 페이저

페이저는 정현파의 진폭과 위상을 표현하는 복소수이다.
페이저는 정현파를 종래의 코사인함수와 사인함수보다 더 편리하고 쉽게 표현할 수 있다.

 

 

페이저

페이저는 세가지 형식으로 표현할 수 있다. 위에서부터 차례대로 직각좌표 형식, 극좌표 형식, 지수 형식이라 한다. 여기서 r은 z의 크기, Φ는 z의 위상이다.

각 형식은 서로 치환이 가능하다. 만약 x와 y가 주어지면 다음과 같이 r과 Φ를 구할 수 있다. 여기서 x축은 복소수의 실수부를 나타내고 y축은 복소수의 허수부를 나타낸다. 반대로 r과 Φ가 주어지면 x와 y를 구할 수 있다.

그러므로 z는 다음과 같이 쓸 수 있다.

복소수의 계산법

덧셈

뺄셈

곱셈

나눗셈

역수

제곱근

켤레복소수

역수 활용

페이저 표현의 개념은 오일러 함수를 기본으로 한다. 일반적으로 다음과 같다. 실수부와 허수부를 각각 cos(Φ)와 sin(Φ)로 보면 된다. 그러므로 다음과 같이 쓸 수 있다.

그리고 v(t)를 다음과 같이 표현할 수 있다. 또는 그러므로 여기서 V는 정현파 v(t)의 페이저 표현이다.

정현파-페이저 변환                                                     (시간 영역 표현)                                             <->                            (페이저 영역 표현)

v(t)를 미분해보면 다음과 같다. 위를 참고하여 v(t)의 도함수와 적분을 페이저 영역으로 변환하면 다음과 같다. ＃미분 ＃적분

실전문제 9.7

미적분방정식으로 표현된 회로의 전압 v(t)를 페이저를 이용하여 구하라

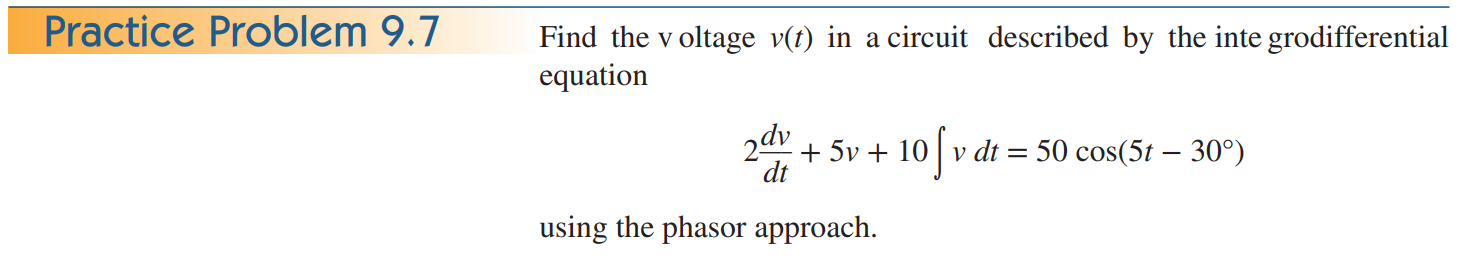
9.4 회로소자의 페이저 관계

위 장에서 주파수 영역에서의 전압과 전류를 페이저 형태로 표현하는 방법을 공부하였다. 이를 수동소자인 R, L, C를 포함하는 회로 해석에 어떻게 적용하는지 알아볼 것이다. 이를 위해 각 소자에 대한 전압-전류의 관계를 시간 영역에서 주파수 영역으로 변환할 것이다.

저항

저항에 흐르는 전류를 I_mcos(ωt + Φ)라 가정하자. 저항 양단에 걸리는 전압은 다음과 같다. 위의 페이저 형태는 다음과 같다. 그러므로 다음과 같이 정리할 수 있다. 페이저 영역이나 시간 영역이나 저항의 전압-전류 관계는 옴의 법칙을 그대로 적용할 수 있다.

인덕터

인덕터를 통해 흐르는 전류가 I_mcos(ωt + Φ)라고 가정하자. 인덕터 양단에 걸리는 전압은 다음과 같다. -sinA = cos(A + 90°)로부터 다음과 같이 표현할 수 있다. 이를 페이저로 변환하면 아래와 같은 식이 나온다. e^j90° = j 이므로 변환하면 아래와 같이 정리할 수 있다.

커패시터

커패시터 양단의 전압이 v = V_mcos(ωt + Φ)이라 가정하자. 커패시터에 흐르는 전류는 다음과 같다. 인덕터에서 적용한 방법과 같이 적용하면 다음을 얻을 수 있다.

★페이저 영역 전압-전류 관계 요약★

예제 9.7

0.1H인 인덕터에 전압 v=12cos(60t + 45°)를 인가한다. 인덕터에 흐르는 정상상태 전류를 구하라.

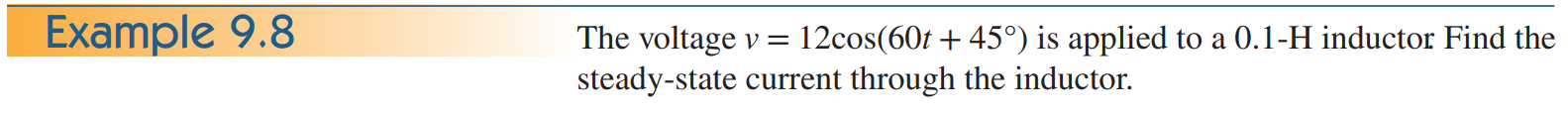
9.5 임피던스와 어드미턴스

앞 절에서 세 가지 수동소자에 대한 전압-전류 관계를 다음과 같이 구했다.

이 관계식은 페이저 전압과 페이저 전류의 비를 이요하여 표현하면 다음과 같다.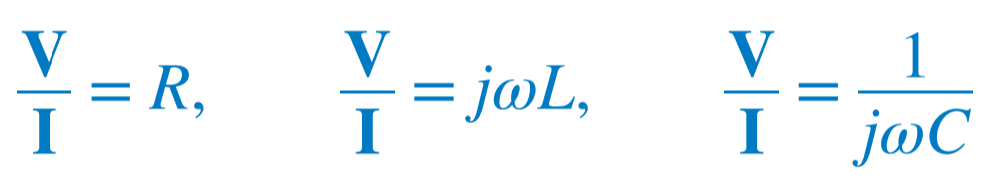

위의 표현으로부터 각 소자에 대해 페이저 형태의 옴의 법칙을 얻을 수 있다.

회로의 임피던스 Z는 페이저 전압 V와 페이저 전류 I의 비이며, 단위는 옴(Ω)이다.

수동소자의 임피던스와 어드미턴스

임피던스

임피던스는 복소량으로 다음과 같이 직각좌표 형식으로 표현할 수 있다. 여기서 R = Re Z는 저항, X = Im Z는 리액턴스이다. 벡터로 사용되는 경우에는 j가 인덕턴스와 관련되고 -j는 커패시턴스와 관련된다.

임피던스는 다음과 같이 극좌표 형식으로도 표현할 수 있다. 그래서 한번에 정리하면 다음과 같다. 그리고 다음과 같이 정리된다. 그리고 여기서 임피던스의 역수인 어드미턴스를 사용하는 것이 편리한 경우도 있다.

어드미턴스 Y는 임피던스의 역수이며, 단위는 지멘스(S)이다.

어드미턴스

소자 혹은 회로의 어드미턴스 Y는 소자를 통해 흐르는 페이저 전류와 소자의 양단에 걸리는 페이저 전압의 비이다.

어드미턴스는 복소량이므로 Y를 다음과 같이 표현할 수 있다.

여기서 G = Re Y는 컨덕턴스라 부르고, B = Im Y는 서셉턴스라 부른다.

임피던스 Z와 어드미턴스 Y는 역수 관계이므로 다음 관계식이 성립한다.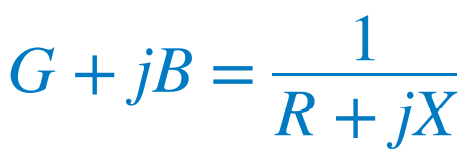 유리화를 통해 정리하게 되면, 실수부와 허수부는 다음과 같다.(G != 1/R) 이로 인해 임피던스와 어드미턴스의 실수부와 허수부도 각각 정리할 수 있다.